Designing a Language

Building a language and an interpreter for it from scratch

Project maintained by FallenDeity Hosted on GitHub Pages — Theme by mattgraham

Parsing

Introduction

In the previous step we have created a lexer that can tokenize our input. Now we need to parse the tokens and create an AST (Abstract Syntax Tree) from them. The AST is a tree representation of the source code. An AST is a more richer and comprehensive representation of the source code than the tokens which allows us to evaluate the code and generate the output. Regular/linear language formats like a stream of tokens cannot be used for complex expressions due to multiple variations of the same expression. Hence we need a more complex representation to handle arbitrary levels of nesting and precedence.

AST

Grammar

The grammar of a language is a set of rules that define the syntax of the language.

Our language Lox will contain the following Grammar expressions:

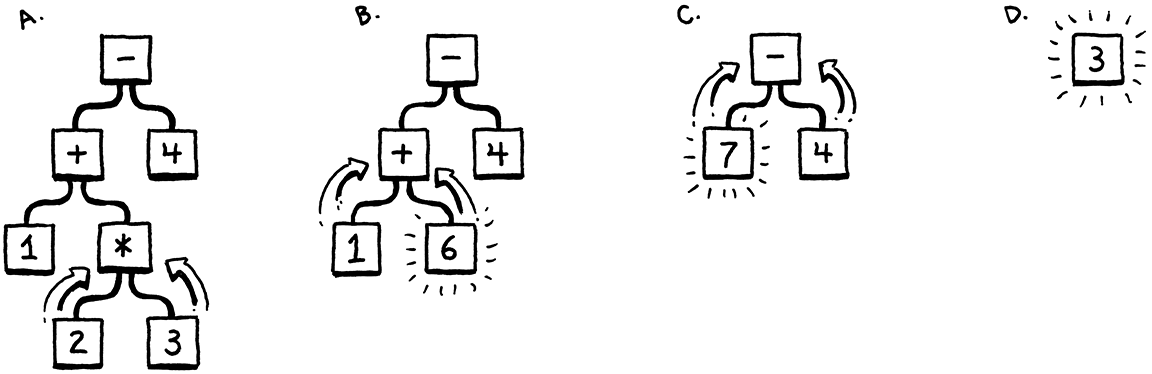
Now take for example the following expression:

Grammar

The above expression can be represented as a tree in the following ways:

Tree

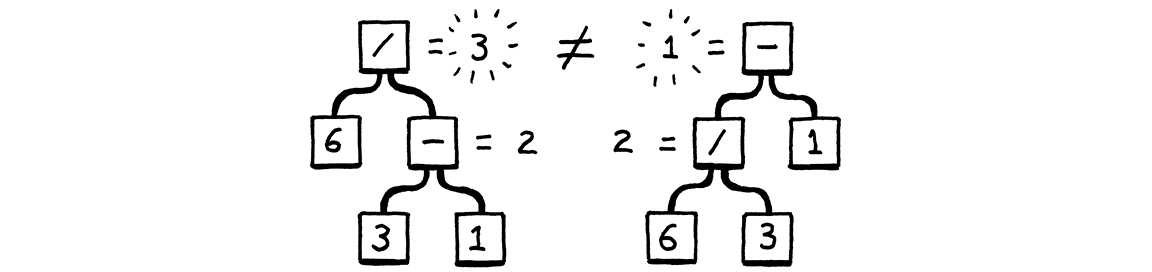
Both of the above are valid representations of the expression. So how do we know which one is correct? We need to define a set of rules that will enforce the correct representation of the expression. These rules are called Grammar Rules. This is exactly what mathematicians did with the Order of Operations rule. The Order of Operations rule states that the multiplication and division operations should be performed before the addition and subtraction operations. This rule enforces the first representation of the expression as the correct one.

And this is exactly what we will do with our language. We will define a set of rules that will enforce the correct representation of the expression.

expression     → ...
equality       → ...
comparison     → ...
term           → ...
factor         → ...
unary          → ...
primary        → ...

You will see how these rules are enforced in the following sections.

ℹ️ Note Definition of the data models can be found here

Now that we know what expressions we need to support, we can define the grammar rules for them. The grammar rules are defined using a notation called Backus-Naur Form (BNF). BNF is a notation for expressing context-free grammars. A context-free grammar is a set of recursive rules used to generate patterns of strings.

The following is the BNF notation for our language:

program        → declaration* EOF ;

declaration    → classDecl
               | funDecl
               | varDecl
               | statement ;

classDecl      → "class" IDENTIFIER ( "<" IDENTIFIER )?  // Inheritance
                 "{" function* "}" ;

funDecl        → "fun" function ;

varDecl        → "var" IDENTIFIER ( "=" expression )? ";" ;

statement      → exprStmt
               | forStmt
               | ifStmt
               | printStmt
               | returnStmt
               | whileStmt
               | block
               | breakStmt
               | continueStmt ;  

exprStmt       → expression ";" ;

The * symbol means that the preceding element can be repeated zero or more times. The | symbol means that the preceding element is optional. The ? symbol means that the preceding element can be repeated zero or one times.

Parsing

Now that we have defined the grammar rules, we can start parsing the tokens. We will use a technique called Recursive Descent Parsing to parse the tokens. Recursive descent parsing is a top-down parsing technique that constructs the parse tree from the top and the input is read from left to right. The parser starts with the start symbol and recursively parses the input until it matches the start symbol.

Recursive Descent Parsing

Let’s start by defining the Parser class:

class Parser:
    def __init__(self, tokens: list["Token"], logger: "Logger", source: str, debug: bool = True) -> None:
        self._tokens = tokens
        self._current = 0
        self._logger = logger
        self._debug = debug
        self._source = source
        self._has_error = False

    def _previous(self) -> "Token":
        """Get the previous token."""
        return self._tokens[self._current - 1]

    def _peek(self) -> "Token":
        """Get the current token."""
        return self._tokens[self._current]

    def _is_at_end(self) -> bool:
        """Check if the parser is at the end of the tokens."""
        return isinstance(self._peek().token_type, EOFTokenType)

    def _advance(self) -> "Token":
        """Advance the parser."""
        if not self._is_at_end():
            self._current += 1
        return self._previous()

    def _check(self, token_type: "TokenType") -> bool:
        """Check if the current token is of a certain type."""
        if self._is_at_end():
            return False
        return self._peek().token_type == token_type

    def _match(self, *token_types: "TokenType") -> bool:
        """Check if the current token is of any of the given types."""
        for token_type in token_types:
            if self._check(token_type):
                self._advance()
                return True
        return False

This is the base parser class that we will use to parse the tokens. The parser class contains the following methods to help us parse the tokens:

Enforce grammar rules

To enforce the grammer rules such an eol after a statement, we will define a _consume() method that will consume the current token if it is of the given type. If the current token is not of the given type, we will report an error and synchronize the parser by skipping tokens until we reach a statement boundary.

    def _error(self, token: "Token", error: str, message: str) -> None:
        line = self._source.splitlines()[token.line - 1]
        if not self._debug:
            self._logger.error(f"{error}\n{message}\n{line}\n{'~' * (token.column - 1)}^")
        raise PyLoxParseError(f"{error}\n{message}\n{line}\n{'~' * (token.column - 1)}^")

    def _consume(self, token_type: "TokenType", message: str) -> "Token":  # type: ignore
        """Consume a token."""
        token = self._previous()
        if self._check(token_type):
            return self._advance()
        error = f"Expected {str(token_type)} but got {str(token.token_type)} in {token.line - self._lox._process.lines}:{token.column}"
        self._error(token, error, message)

This neat little method will consume the current token if it is of the given type. If the current token is not of the given type, we will report an error and synchronize the parser by skipping tokens until we reach a statement boundary. This allows us to expect a certain token type like ; after a statement , between arguments, etc.

Parse expressions

Now that we have defined the base parser class, we can start parsing the tokens.

Lets write our basic parse function:

    def parse(self) -> list["Stmt"]:
        """Parse the tokens."""
        statements: list["Stmt"] = []
        while not self._is_at_end():
            if (decl := self._declaration()) is not None:
                statements.append(decl)
        return statements

In this context Stmt stands for Statement. A statement is a single instruction that can be executed. A statement can be a declaration, an expression, a control flow statement, etc. Since we are making a recursive descent parser, we will start with the top level rule program and recursively parse the tokens until we reach the end of the tokens.

Here we continue parsing the tokens until we reach the end of the tokens. We check if the current token is a declaration and if it is, we parse it and add it to the list of statements.

Now that we have defined the basic parse function, we can divide statements into different categories and parse them accordingly.

Now that we have divided the statements into different categories, we can start parsing them.

    def _declaration(self) -> Stmt | None:
        """Parse a declaration."""
        try:
            if self._match(KeywordTokenType.VAR):
                return self._var_declaration()
            elif self._match(KeywordTokenType.FUN):
                return self._function_declaration("function")
            elif self._match(KeywordTokenType.CLASS):
                return self._class_declaration()
            return self._statement()
        except PyLoxParseError as e:
            if self._debug:
                self._error(self._peek(), "Parse Error", str(e))
            self._has_error = True
            self._synchronize()
            return None

Before we head over to parsing the statements, we need to handle errors. We will use a technique called Error Recovery to handle errors. Error recovery is a technique used to recover from errors in a parser. When an error is encountered, the parser will try to recover from the error and continue parsing the tokens. We will use a technique called Panic Mode to recover from errors. Panic mode is a technique used to recover from errors by skipping tokens until we reach a token that we can use to continue parsing the tokens. We are doing this instead of raising an error because we want to show all the errors in the code instead of just the first error that we encounter. Modern ides like VSCode and PyCharm use this technique to show all the errors in the code.

So now to the question of how do we know when to stop skipping tokens? We will use a technique called Synchronization to know when to stop skipping tokens.

    def _synchronize(self) -> None:
        """Synchronize the parser."""
        self._advance()
        while not self._is_at_end():
            if self._previous().token_type == SimpleTokenType.SEMICOLON:  # skip to the next statement if we encounter a semicolon ';'
                return
            if self._peek().token_type in (  # skip to the next statement if we encounter a keyword that starts a statement
                KeywordTokenType.CLASS,
                KeywordTokenType.FUN,
                KeywordTokenType.VAR,
                KeywordTokenType.FOR,
                KeywordTokenType.IF,
                KeywordTokenType.WHILE,
                KeywordTokenType.PRINT,
                KeywordTokenType.RETURN,
                KeywordTokenType.THROW,
            ):
                return
            self._advance()

Now for the few of you observant ones what will happen if we don’t raise an error won’t we get a bunch of errors? Yes, we will get a bunch of errors but once the parser finishes parsing the tokens, we will raise an error.

Now that we have handled errors, we can start parsing the statements.

Variable declaration

    def _var_declaration(self) -> Var:
        """
        Parse a variable declaration.
        :return: The parsed data
        """
        name = self._consume(LiteralTokenType.IDENTIFIER, "Expected variable name.")
        initializer = None
        if self._match(ComplexTokenType.EQUAL):
            initializer = self._assignment()  # parse the initializer
        self._consume(SimpleTokenType.SEMICOLON, "Expected ';' after variable declaration.")
        return Var(name, initializer)

What we are doing here is that we are parsing the variable name and if there is an initializer we parse it and return the parsed data. We detect a variable declaration by checking if the current token is of type var and if it is we parse the variable declaration. If the identifier is followed by an equal sign = we parse the initializer and return the parsed data.

Function declaration

    def _function_declaration(self, kind: str) -> Function:
        """
        Parse a function declaration.
        :param kind: The kind of function
        :return: The parsed data
        """
        name = self._consume(LiteralTokenType.IDENTIFIER, f"Expected {kind} name.")
        self._consume(SimpleTokenType.LEFT_PAREN, f"Expected '(' after {kind} name.")
        parameters: list["Token"] = []
        if not self._check(SimpleTokenType.RIGHT_PAREN):
            while True:
                if len(parameters) >= 255:
                    self._error(
                        self._peek(), "Parse Error", f"Cannot have more than 255 parameters in {kind} {name.lexeme}"
                    )
                parameters.append(self._consume(LiteralTokenType.IDENTIFIER, "Expected parameter name."))
                if not self._match(SimpleTokenType.COMMA):
                    break
        self._consume(SimpleTokenType.RIGHT_PAREN, "Expected ')' after parameters.")
        self._consume(SimpleTokenType.LEFT_BRACE, "Expected '{' before" + f" {kind} body.")
        body = self._block()
        return Function(name, parameters, body)

What we are doing here is that we are parsing the function name and the parameters and if there is a body we parse it and return the parsed data. We detect a function declaration by checking if the current token is of type fun and if it is we parse the function declaration. If the identifier is followed by a ( we parse the parameters and if there is a { we parse the body and return the parsed data.

Class Declaration

    def _class_declaration(self) -> Class:
        """
        Parse a class declaration.
        :return: The parsed data
        """
        name = self._consume(LiteralTokenType.IDENTIFIER, "Expected class name.")
        super_class = None
        if self._match(ComplexTokenType.LESS):
            self._consume(LiteralTokenType.IDENTIFIER, "Expected superclass name.")
            super_class = Variable(self._previous())
        self._consume(SimpleTokenType.LEFT_BRACE, "Expected '{' before class body.")
        methods: list[Function] = []
        while not self._check(SimpleTokenType.RIGHT_BRACE) and not self._is_at_end():
            methods.append(self._function_declaration("method"))
        self._consume(SimpleTokenType.RIGHT_BRACE, "Expected '}' after class body.")
        return Class(name, super_class, methods)

Class declaration is similar to function declaration. We parse the class name and the superclass and if there is a body we parse it and return the parsed data. The only difference is that we parse the methods inside the class. We detect a class declaration by checking if the current token is of type class and if it is we parse the class declaration. If the identifier is followed by a { we parse the methods and return the parsed data.

Statements

    def _statement(self) -> Stmt:
        """
        Parse a statement.
        :return: The parsed data
        """
        if self._match(KeywordTokenType.FOR):
            return self._for_statement()
        elif self._match(KeywordTokenType.IF):
            return self._if_statement()
        elif self._match(KeywordTokenType.PRINT):
            return self._print_statement()
        elif self._match(KeywordTokenType.RETURN):
            return self._return_statement()
        elif self._match(KeywordTokenType.WHILE):
            return self._while_statement()
        elif self._match(KeywordTokenType.BREAK):
            return self._break_statement()
        elif self._match(KeywordTokenType.CONTINUE):
            return self._continue_statement()
        elif self._match(KeywordTokenType.THROW):
            return self._throw_statement()
        elif self._match(KeywordTokenType.TRY):
            return self._try_statement()
        elif self._match(SimpleTokenType.LEFT_BRACE):
            return Block(self._block())
        return self._expression_statement()

Finally, we have reached the most important part of the parser. The statement parser. The statement parser is the most important part of the parser because it is the one that parses the statements. The statement parser is a recursive descent parser. A recursive descent parser is a top-down parser built from a set of mutually recursive procedures (or a non-recursive equivalent) where each such procedure usually implements one of the productions of the grammar. Thus the structure of the resulting program closely mirrors that of the grammar it recognizes. Recursive descent parsing is one of the simplest parsing techniques. It requires a separate procedure for each rule of the grammar. The term “recursive descent” refers to the fact that the parser calls itself recursively to parse some piece of the input.

Now explaining declaration of each possible statement is out of the scope of this tutorial. So I will just explain the if statement and the while statement and try to give a brief idea of how the other statements are parsed.

Lets start with the if statement.

    def _if_statement(self) -> Stmt:
        """
        Parse an if statement.
        :return: The parsed data
        """
        self._consume(SimpleTokenType.LEFT_PAREN, "Expected '(' after 'if'.")  # consume the '('
        condition = self._assignment()  # If there is an expression parse it
        self._consume(SimpleTokenType.RIGHT_PAREN, "Expected ')' after if condition.")  # consume the ')'
        then_branch = self._statement()  # parse the then branch it can be a statement or a block essentially block is a list of statements
        else_branch = None
        if self._match(KeywordTokenType.ELSE):  # if there is an else branch parse it
            else_branch = self._statement()  # same as then branch
        return If(condition, then_branch, else_branch)  # return the parsed data

What we are doing here is that we are parsing the condition and if there is a then branch we parse it and if there is an else branch we parse it and return the parsed data.

    def _while_statement(self) -> Stmt:
        """
        Parse a while statement.
        :return: The parsed data
        """
        self._consume(SimpleTokenType.LEFT_PAREN, "Expected '(' after 'while'.")  # consume the '('
        condition = self._assignment()  # If there is an expression parse it
        self._consume(SimpleTokenType.RIGHT_PAREN, "Expected ')' after condition.") # consume the ')'
        body = self._statement()  # parse the body it can be a statement or a block
        return While(condition, body)

As you can see above we are just enforcing the grammar rules of the language. Our main atomic parsing units remain in the form of expressions. We are recursively calling few functions to parse the expressions and form meaningful statements.

Parser Functions

    def _assignment(self) -> Expr:
        """
        Parse an assignment.
        :return: The parsed data
        """
        expr = self._or()  # parse the left hand side
        if self._match(ComplexTokenType.EQUAL):  # if there is an equal sign parse the right hand side
            value = self._assignment()  # parse the right hand side
            if isinstance(expr, Variable):  # if the left hand side is a variable
                name = expr.name  # get the name of the variable
                return Assign(name, value)  # return the parsed data
            elif isinstance(expr, Get):  # if the left hand side is a get expression `a.b = 1`
                return Set(expr.object, expr.name, value)  # return the parsed data
            self._error(self._previous(), "Invalid assignment target.", "Cannot assign to this expression.")
        return expr  # return the parsed data

Deal with assignment. Assignment is a binary operator. So we parse the left hand side and then we check if the current token is of type =. If it is we parse the right hand side and return the parsed data.

    def _or(self) -> Expr:
        """
        Parse an or expression.
        :return: The parsed data
        """
        expr = self._and()  # parse the left hand side
        while self._match(KeywordTokenType.OR):  # if there is an or operator parse the right hand side
            operator, right = self._previous(), self._and()  # parse the right hand side
            expr = Logical(expr, operator, right)  # return the parsed data
        return expr  # return the parsed data

Parse an or expression. Or is a binary operator. So we parse the left hand side and then we check if the current token is of type or. If it is we parse the right hand side and return the parsed data.


    def _and(self) -> Expr:
        """
        Parse an and expression.
        :return: The parsed data
        """
        expr = self._equality()  # parse the left hand side
        while self._match(KeywordTokenType.AND):  # if there is an and operator parse the right hand side
            operator, right = self._previous(), self._equality()  # parse the right hand side
            expr = Logical(expr, operator, right)  # return the parsed data
        return expr  # return the parsed data

Parse an and expression. And is a binary operator. So we parse the left hand side and then we check if the current token is of type and. If it is we parse the right hand side and return the parsed data.

    def _equality(self) -> Expr:
        """
        Parse an equality expression.
        :return: The parsed data
        """
        expr = self._comparison()  # parse the left hand side
        while self._match(ComplexTokenType.BANG_EQUAL, ComplexTokenType.EQUAL_EQUAL):  # if there is an equality operator parse the right hand side
            operator, right = self._previous(), self._comparison()  # parse the right hand side
            expr = Binary(expr, operator, right)  # return the parsed data
        return expr  # return the parsed data

Parse an equality expression. Equality is a binary operator. So we parse the left hand side and then we check if the current token is of type != or ==. If it is we parse the right hand side and return the parsed data.

    def _comparison(self) -> Expr:
        """
        Parse a comparison expression.
        :return: The parsed data
        """
        expr = self._term()  # parse the left hand side
        while self._match(
            ComplexTokenType.GREATER, ComplexTokenType.GREATER_EQUAL, ComplexTokenType.LESS, ComplexTokenType.LESS_EQUAL
        ):  # if there is an comparison operator parse the right hand side
            operator, right = self._previous(), self._term()  # parse the right hand side
            expr = Binary(expr, operator, right)  # return the parsed data
        return expr  # return the parsed data

Parse a comparison expression. Comparison is a binary operator. So we parse the left hand side and then we check if the current token is of type >, >=, < or <=. If it is we parse the right hand side and return the parsed data.

    def _term(self) -> Expr:
        """
        Parse a term expression.
        :return: The parsed data
        """
        expr = self._factor()  # parse the left hand side
        while self._match(SimpleTokenType.MINUS, SimpleTokenType.PLUS):  # if there is an term operator parse the right hand side
            operator, right = self._previous(), self._factor()  # parse the right hand side
            expr = Binary(expr, operator, right)  # return the parsed data
        return expr  # return the parsed data

Parse a term expression. Term is a binary operator. So we parse the left hand side and then we check if the current token is of type - and +. If it is we parse the right hand side and return the parsed data. For example 1 + 2 - 3 is parsed as 1 + (2 - 3). This is because - has higher precedence than +.

    def _factor(self) -> Expr:
        """
        Parse a factor expression.
        :return: The parsed data
        """
        expr = self._unary()  # parse the left hand side
        while self._match(SimpleTokenType.CARAT, SimpleTokenType.SLASH, ComplexTokenType.BACKSLASH, SimpleTokenType.STAR, SimpleTokenType.MODULO):  # if there is an factor operator parse the right hand side
            operator, right = self._previous(), self._unary()  # parse the right hand side
            expr = Binary(expr, operator, right)  # return the parsed data
        return expr  # return the parsed data

Parse a factor expression. Factor is a binary operator. So we parse the left hand side and then we check if the current token is of type ^, /, \\, * and %. If it is we parse the right hand side and return the parsed data. For example 1 * 2 / 3 is parsed as 1 * (2 / 3). This is because / has higher precedence than *.

    def _unary(self) -> Expr:
        """
        Parse a unary expression.
        :return: The parsed data
        """
        if self._match(SimpleTokenType.BANG, SimpleTokenType.MINUS):  # if there is an unary operator parse the right hand side
            operator, right = self._previous(), self._unary()  # parse the right hand side
            return Unary(operator, right)  # return the parsed data
        return self._call()  # if none of the above expressions match that means it not a binary expression so we parse the call expression

Parse a unary expression. Unary is a unary operator. So we check if the current token is of type ! and -. If it is we parse the right hand side and return the parsed data.

    def _call(self) -> Expr:
        """
        Parse a call expression.
        :return: The parsed data
        """
        expr = self._primary()  # parse the left hand side
        assert isinstance(expr, Expr)
        while True:
            if self._match(SimpleTokenType.LEFT_PAREN):  # if there is an call operator parse the right hand side
                expr = self._finish_call(expr)  # parse the right hand side
            elif self._match(SimpleTokenType.DOT):  # if there a dot operator parse the right hand side
                name = self._consume(LiteralTokenType.IDENTIFIER, "Expected property name after '.'.")  # make sure there is a property name like `foo.bar`
                expr = Get(expr, name)  # parse the right hand side
            else:
                break
        return expr  # return the parsed data

This function does two things. It parses a call expression and a dot expression. For example foo.bar() which is a call expression and foo.bar which is a dot expression.

    def _finish_call(self, callee: Expr) -> Expr:
        """
        Finish parsing a call expression.
        :param callee: The callee
        :return: The parsed data
        """
        arguments: list[Expr] = []  # create a list to store the arguments
        if not self._check(SimpleTokenType.RIGHT_PAREN):  # if there are arguments
            while True:  # loop through the arguments
                if len(arguments) >= 255:  # make sure there are not more than 255 arguments
                    self._error(self._peek(), "Cannot have more than 255 arguments.", "\n")  # raise an error
                arguments.append(self._assignment())  # parse the argument
                if not self._match(SimpleTokenType.COMMA):  # if there are no more arguments
                    break  # break out of the loop
        paren = self._consume(SimpleTokenType.RIGHT_PAREN, "Expected ')' after arguments.")  # make sure there is a closing parenthesis
        return Call(callee, paren, tuple(arguments))  # return the parsed data

In the case it is a call expression we parse the arguments and return the parsed data. For example foo(1, 2, 3) is parsed and [1, 2, 3] is returned.

    def _primary(self) -> Expr | None:
        """
        Parse a primary expression.
        :return: The parsed data
        """
        if self._match(KeywordTokenType.LAMBDA):  # if it is a lambda expression `lambda x: x`
            return self._lambda()
        if self._match(KeywordTokenType.FALSE):  # if it is a false expression `false`
            return Literal(False)
        if self._match(KeywordTokenType.TRUE):  # if it is a true expression `true`
            return Literal(True)
        if self._match(KeywordTokenType.NIL):  # if it is a nil expression `nil`
            return Literal(None)
        if self._match(LiteralTokenType.NUMBER, LiteralTokenType.STRING):  # if it is a number or string expression `1` or `"foo"`
            return Literal(self._previous().literal)
        if self._match(KeywordTokenType.SUPER):  # if it is a super expression `super.foo`
            keyword = self._previous()
            self._consume(SimpleTokenType.DOT, "Expected '.' after 'super'.")
            method = self._consume(LiteralTokenType.IDENTIFIER, "Expected superclass method name.")
            return Super(keyword, method)
        if self._match(KeywordTokenType.THIS):  # if it is a this expression `this` this is the same as `self`
            return This(self._previous())
        if self._match(LiteralTokenType.IDENTIFIER):  # if it is a identifier expression `foo`
            return Variable(self._previous())
        if self._match(SimpleTokenType.LEFT_PAREN):  # if it is a grouping expression `(1 + 2)`
            expr = self._assignment()
            self._consume(SimpleTokenType.RIGHT_PAREN, "Expected ')' after expression.")
            return Grouping(expr)
        self._error(self._peek(), f"Expected expression. Got '{self._peek().lexeme}'.", "Invalid expression.")

This function parses all the primary expressions. Primary expressions are expressions that cannot be broken down further. For example 1 is a primary expression. It cannot be broken down further. It is just a number.

Now that we have completed our parser we can test it out.

>>> var x = 7;
[2023-04-30 00:18:48,991] | ~\src\interpreter\lox.py:39 | INFO | Running PyLox...
[Var(name=Token(self.token_type=<LiteralTokenType.IDENTIFIER: 'identifier'>, self.lexeme='x', self.literal='x', self.line=1, self.column=6), initializer=Literal(value=7))]
[2023-04-30 00:18:48,992] | ~\src\interpreter\lox.py:52 | INFO | Finished running PyLox.

Hooraay! We have successfully made a parser. Give yourself a pat on the back. You deserve it.

Previous: Language Next: Environment